线性回归,在做简单的数据分析时是最常用到的手段。
如果线性拟合不管用了?——那个时候再去考虑试试别的算法好了。
线性回归是回归问题中经常用到的一种算法。
这在某种意义上有点像在解决求解一次方程系数的初级数学题,但却远比这要复杂得多。
首先,这些点其实并不在一条直线上,而是离散的状态,甚至有时候你很难想象把这些混乱的点拟合成一条直线是否是明智之举。
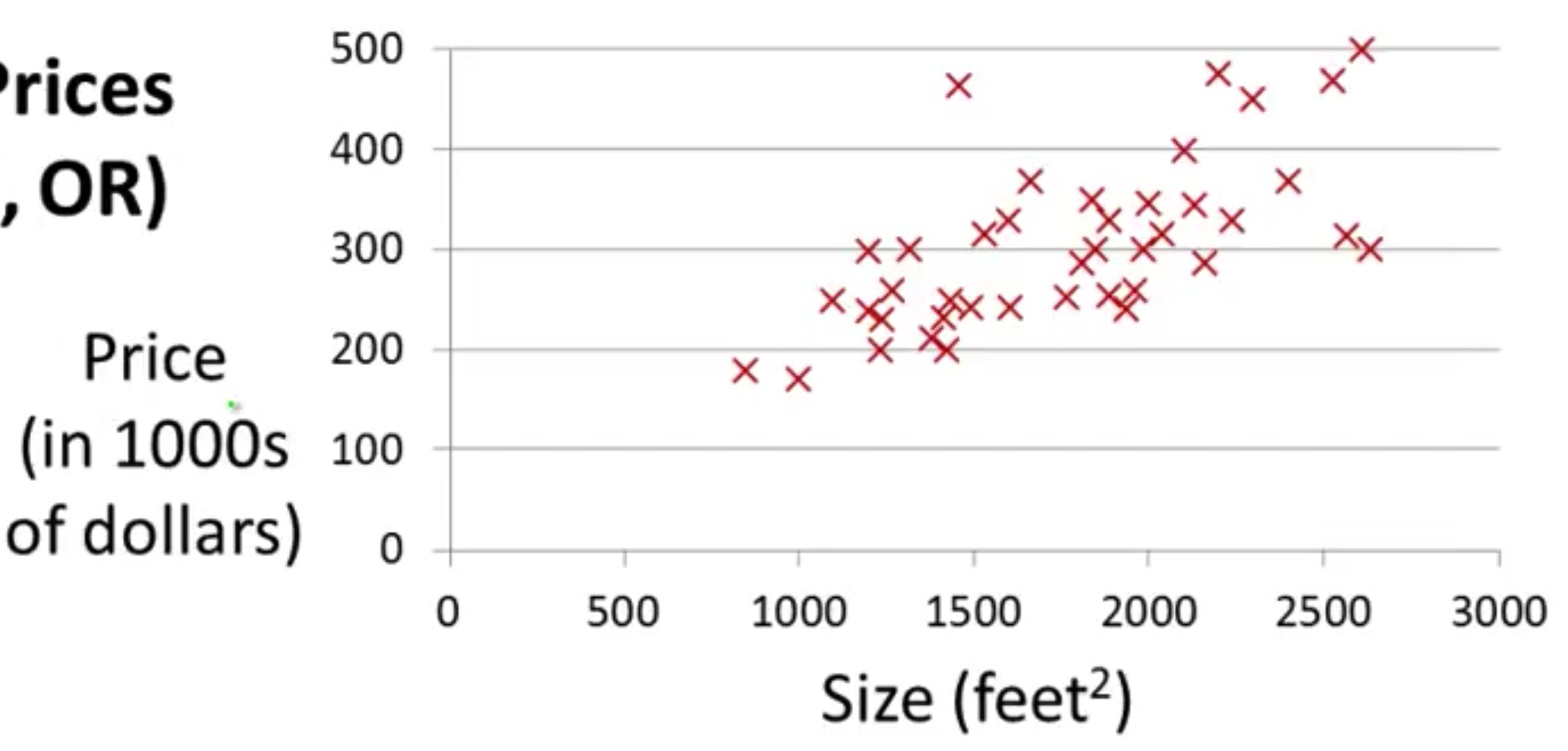
不过,我们还是希望能这么做。
假想函数-Hypothesis Function
我们先明确一些符号所代表的含义:
- $ (x^{i},y^{i}) $:第 $i$ 组数据,$m$ 则代表所有训练数据的总数(就是图中所有点的个数)
- $ h(x) = θ_0+θ_1x $:假想拟合出的线性回归函数。
- $ θ_0、θ_1 $:特征系数,每个特征系数对应一个特征参数 $x_i$,$θ_0$ 比较特殊,本身对应着一个特殊的特征参数 $x_0$,只是 $x_0=1$ 罢了
在建立假想函数之前,我们需要有一个概念:真实数据总是伴随着各种各样的随机性,从而呈现出让人捉摸不透的分布,但在离散的分布中必然存在着合理的函数关系。假想函数正是以此为前提,假定出的符合数学规律并且尽量贴合实际数据的函数关系。
这里稍微发散一下,假想函数和数据集是对应的,如果给定的数据集有两个特征参数(比如房价参考特征除了房间面积外还有房间间数),那么就会有:
- 数据集的表示:$ (x_1^i,x_2^{i},y^{i}) $
- 假想函数的表示:$ h(x) = θ_0+θ_1x_1+θ_2x_2 $
代价函数-Cost Function
这个假想函数不会是随手画的,必须有一个用来矫正这条线的函数,这就是代价函数:
$$ J(θ_0,θ_1) = \frac 1 {2m} \sum _{i=1}^m(h_θ(x_i)-y_i)^2 $$
这种形式的公式倒不陌生,很像方差公式,而方差是体现一组数据离散程度的指标,所以这样定义的代价函数也并不是没有道理的。
我们知道,方差越小,数据越集中。因此,在这里换个说法就是:
代价函数越小,图中的点离假想函数越集中。找到代价函数的最小值,就是我们的假想函数的终点。
求函数的极小值
从Pro.Ng的讲解中,我突然想到了牛顿迭代。
看这幅图:
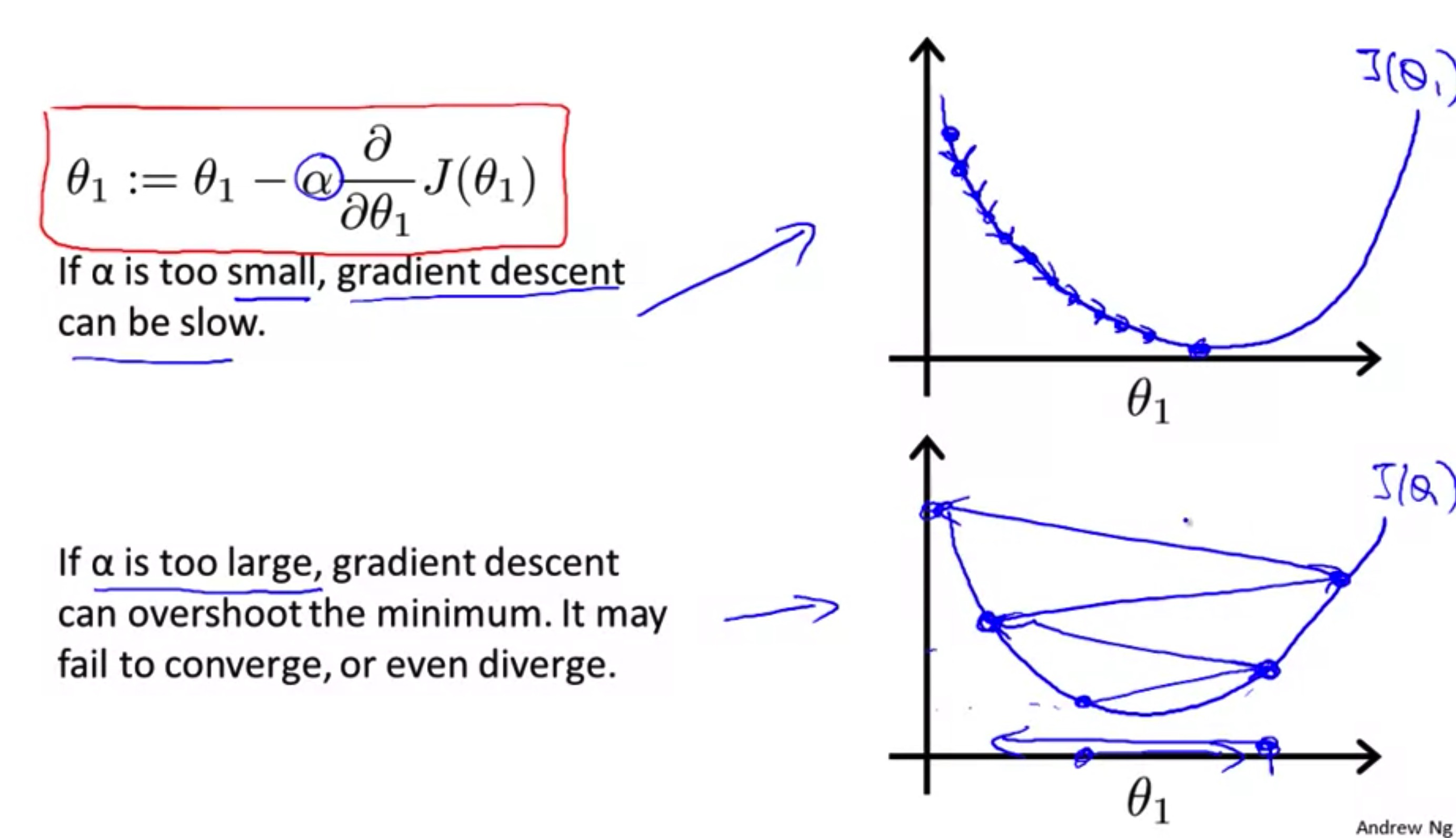
还有当初用来演示牛顿迭代的动画:
没必要刻意去理解导数,从图形直观完全可以理解这样做的道理。
导数,只是一个工具而已。
梯度下降-Gradient Descent
梯度下降实际上是对每一个特征系数‘分别’、’’同时’进行迭代

一次梯度下降的顺序:
- 对系数 $θ_0$ 下降:$ θ_{0_temp}:=θ_0-α\frac δ {δθ_0}J(θ_0,θ_1) $,$ θ_1 $ 看作常量
- 对系数 $θ_1$ 下降:$ θ_{1_temp}:=θ_1-α\frac δ {δθ_1}J(θ_0,θ_1) $,$ θ_0 $ 看作常量
- 对系数 $θ_0$ 赋值:$ θ_0:=θ_{0_{temp}}$
- 对系数 $θ_1$ 赋值:$ θ_1:=θ_{1_{temp}}$
记住,始终将所有特征系数作为一组,用前一组系数去计算下一组的系数,计算完后再赋值。