花点时间,探索一下SVM背后的数学。
从一个简单的例子开始:
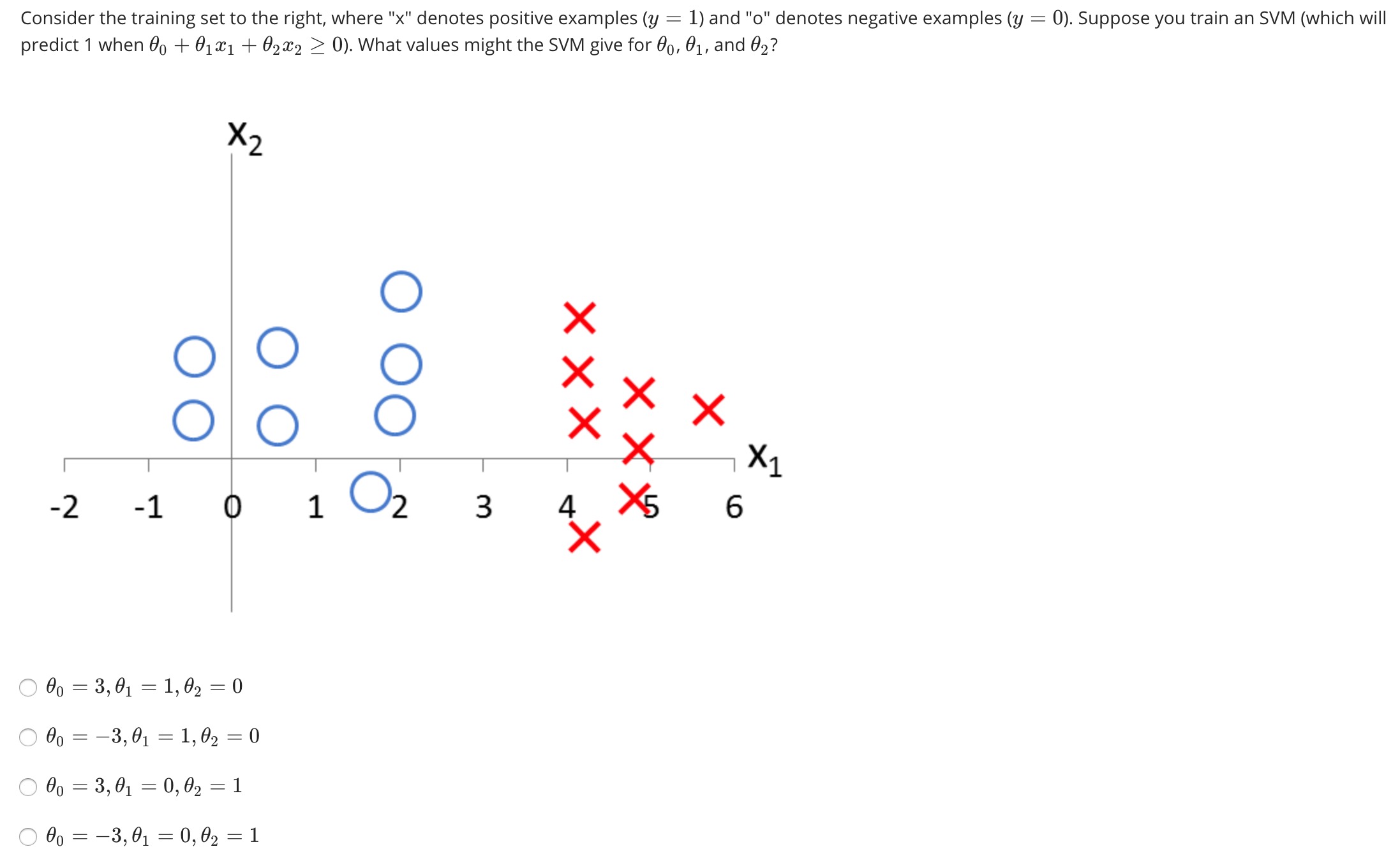
直观上 $x=3$ 的线就可以很好的划分,也就是说,对于所有 $x_1=3,\ x_2 \in R$ 的点,应该有:
$$
\theta_0 + \theta_1x_1+\theta_2x_2=0
$$
典型的“恒成立”问题,则有 $\theta_2=0,\ \theta_0 = -3 \theta_1$
这个再简单不过的线性分类问题就已经有了SVM的思想在里面了。
线性分类器
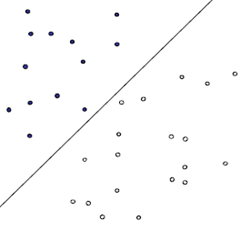
图1对一个线性可分的分类器,一条直线^1就可以简单粗暴地解决,但是分类的效果不一定好,要想得到最好的分类效果,就需要这条线尽可能得宽。楚河汉界,这样的描述再好不过了,如果界限模糊不清,反而会容易产生困扰。
简单比较一下:
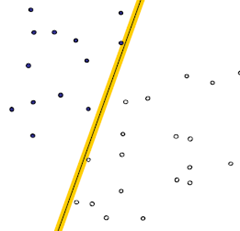
图2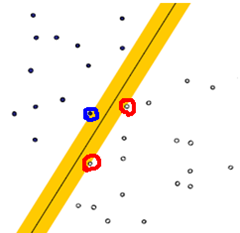
图3图3的分类效果会更好,在图3中标圈的点,我们就称之为“支撑向量”。
我个人的理解:一般来说,支持向量至少为3个,当分类器的两侧边界不足3个点时,就说明还有扩大的余地。
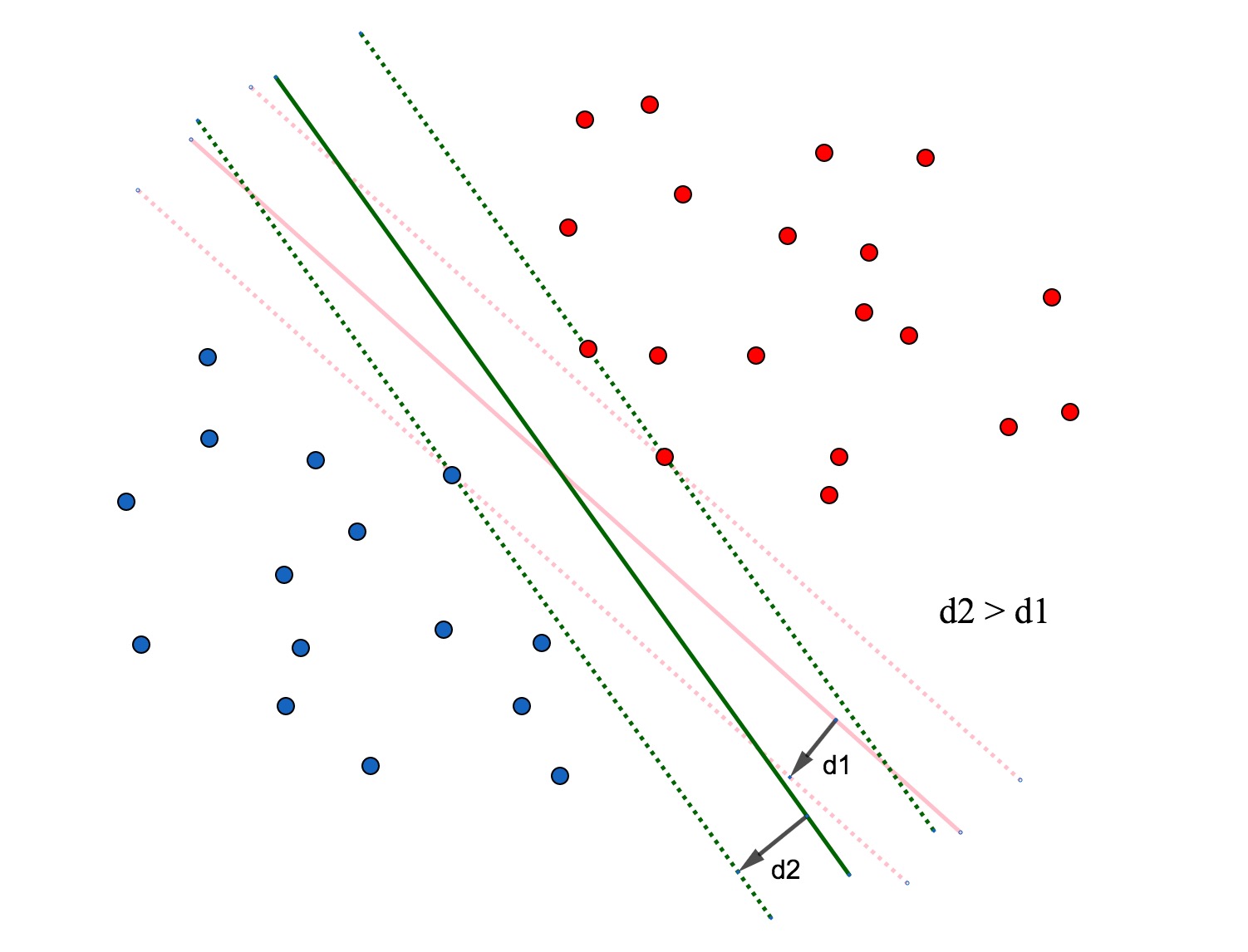
图4问题至此就明确了,我们要找最宽的决策边界对应的线性回归的参数 $w$ 。
边缘最大化
我们先做如下设定:
对这个线性回归问题,$h(x) = wx+b$ 在:
$$
h(x) \ge 1时决策值y=1 \\
h(x) \le -1时决策值y=-1
$$
这里的 1 的取值只是因为二分类问题的正样本和负样本这样取值合理而且便于计算,对后面的优化并没有什么影响。
支持向量所在的点满足:$|wx_i+b|=1$ 。
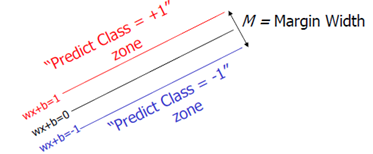
图5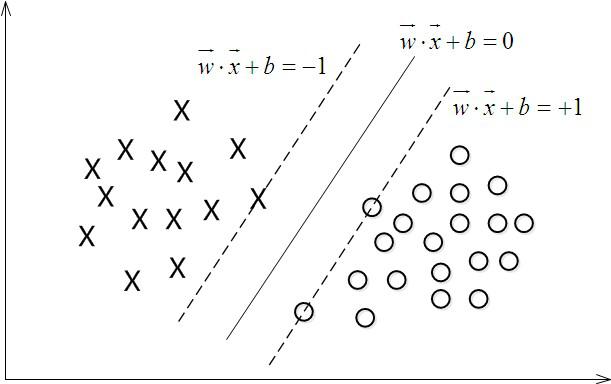
图6图中的 $M$ 就是边距,我们要计算 $M$ 的最大值,即最大边距($Maximum\ Marginal$),这里先给出 $M$ 的式子:
$$
M = \frac 2 {\sqrt {w.w}} = \frac 2 {||w||}
$$
注:$||w||$ 是 $w$ 的二范数。
要理解这个式子,可以先从简单的入手,假定 $w$ 和 $x$ 都是一维的,图5的距离,用简单的数学推导就可以得出:
$$
\begin{align}
&wx_1+b=1 \to x_1=\frac{1-b}w \\
&wx_2+b=-1 \to x_2 = \frac{-1-b}w \\
&d = |x_1-x_2| = \frac2 {|w|}
\end{align}
$$
所以,矩阵的二范数的概念,或许和绝对值的概念很相近也说不定。
言归正传,先说明一下二范数:
$Euclid$范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和的平方根。
在一维(数轴)里,绝对值 $\sqrt{x^2}$ 代表点到原点的距离;
在二维(直角坐标系)里,弦值(勾股定理) $\sqrt{x^2+y^2}$ 也代表点到原点的距离。
不管是绝对值还是弦值,都可以理解为是欧几里得范数,道理其实是一样的,可以说是点到原点的距离,亦或是参数向量 $w$ 的长度。
最终,问题从而演变成了求 $||w||$ 的最小值的问题。
正则项
在吴恩达的机器学习课程中,对SVM的推导是这样进行的:
Logistic Regression:
$$
\min_\theta \frac 1 m \sum _{i=1} ^m [y^{(i)}(-logh_{\theta}(x^{(i)}) + (1-y^{(i)})(-log(1-h_{\theta}(x^{(i)}))] + \frac \lambda {2m} \sum _{j=1} ^n \theta_j^2
$$
将正样本和负样本的误差抽象出来,得到:
Support vector machine:
$$
\min_\theta \frac 1 m \sum _{i=1} ^m [y^{(i)}cost_1(\theta^Tx^{(i)}) + (1-y^{(i)})cost_0(\theta^Tx^{(i)})] + \frac \lambda {2m} \sum _{j=1} ^n \theta_j^2
$$
消除常数项 $\frac 1 m$ ,并将正则项偏差的超参数 $\lambda$ 转移到样本偏差 $C$($C=\frac 1 \lambda$)
Support vector machine:
$$
\min _\theta C \sum _{i=1} ^m [y^{(i)}cost_1(\theta^Tx^{(i)}) + (1-y^{(i)})cost_0(\theta^Tx^{(i)})] + \frac 1 2 \sum _{j=1} ^n \theta_j^2
$$
如果令正样本和负样本在 $|\theta^Tx|\ge1$ 时的误差为 $0$ ,并给 $C$ 一个相当大的值,通过训练 $\theta$ 可以令左侧的项为 $0$
那么最终的目的就成了:
$$
min \frac 1 2 \sum _{j=1} ^n \theta_j^2
$$
这和我们前面讨论的结论是一致的(注意这里的 $ \theta$ 和上面的 $w$ 都是代表机器学习算法的特征参数)。
背后的数学
向量的内积
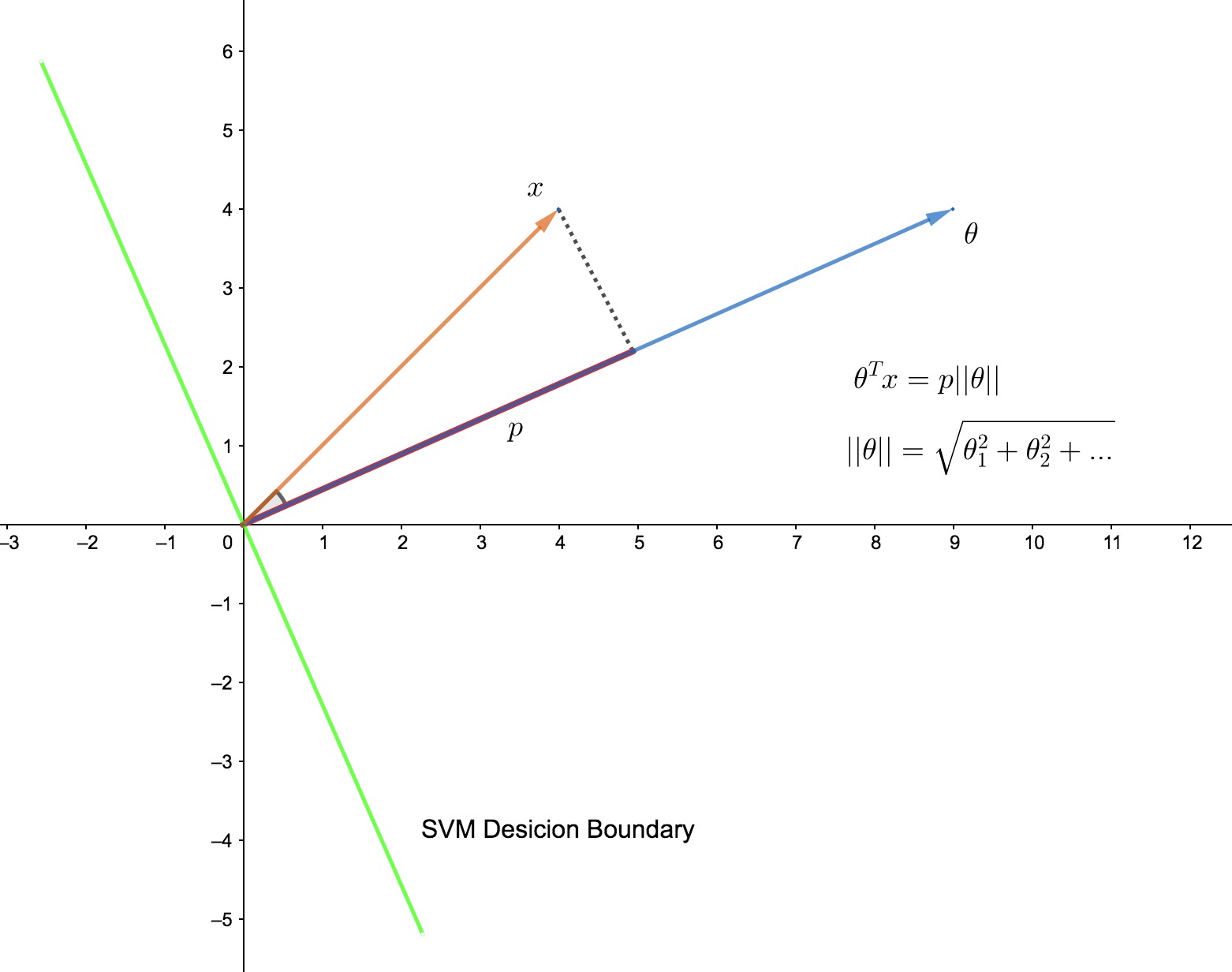
之前讨论过,决策边界是 $wx+b=0$ 的超平面(这里的 $w$ 相当于吴恩达课程中的 $\theta$),如果消除 $b$ 这一项(在吴恩达的课程中,这一项就是 $\theta_0$),则有 $wx=0$,两个向量的内积为 $0$ ,所以两个向量垂直(如图中所示)。
所以对于支持向量,$\theta ^Tx^i = p^i||\theta||$ ,要得到其距离决策边界的最大值,就需要求 $||\theta||$ 的最小值。
小结:SVM问题原型
实际上,这是一个带有约束条件的优化问题,原型的描述是:
$$
\min \frac 1 2 ||w||^2\ \ \ s.t.\ \ \ if\ \ y^{(i)}=1,w^Tx^{(i)} \ge1;if\ \ y^{(i)}=0,w^Tx^{(i)} \le-1
$$
即:在满足 $s.\ t.$ 的条件的同时,得到我们的最优解。
超平面
直接理解“超平面”这样一个数学性很强的概念并不容易,有时候,简化、延伸、归纳可以帮助我们更好地理解。
我们知道,超平面是为了分类我们的数据集的,而数据集一般都是多维的,什么样的东西能一刀划分一个多维的概念呢?我们先从低维开始理解。
比如说有一堆数字:$-38,-25,-8,-4,-3,2,3,5,7,23,16$
怎么划分比较合适呢?最简单的场景,直接以 0 为界分为正数和负数就可以了。

再比如说有一堆点:我们来看开头的例子
再到三维,划分的条件就是一个平面了。
如果再到更高的维度,划分条件就是一个超平面。
$n$ 维空间中的超平面由下面的方程确定:
$$
wx+b=0
$$
消除偏置项 $b$ ,超平面就是 $n$ 维空间的一个子空间(过原点)。