逻辑算法,对分类问题使用的回归算法。
分类问题-$Classification$
分类问题
classification一般会将问题的结果归纳为互不关联的几个类别class
换言之,如果给定一个物体,分类问题需要我们预测这个物体是什么,如果给定A、B、C三个选项,我们则必须给出类似于下面的结论1的表述:
结论1:该物体是
A结论2:该物体是
A的可能性是$P(A)$($P(A)$是概率,在$0\sim1$之间)
而显然结论2的表述更有数学意义,可以用来指导结论1。若:$P(A)$ 比 $P(B)$ 、$P(C)$ 都大,那么我们就预测这个物体是A。
而对于比较简单的二元分类问题(即只有A、B两个选项),一旦得出A的概率 $P(A)$ ,那么B的概率即为 $1-P(A)$ ,即所谓的“非此即彼”,所以我们只需要训练A的概率即可。
那么,如何去求一组训练数据,选项为A的概率呢?这时可能有人要问了——
不就等于:集合 $y$ 中 $A$ 的个数/集合 $y$ 的总数 吗?
这就是经典的本末倒置了。用 $y$ 去预测 $y$ ,不是我们的目的,我们要做的是:当新来一个数据时,能根据给定的条件 $x$ ,去预测 $y$ 。
举个简单的例子,如果现有一组判断肿瘤是良性(
A)还是恶性(B)的训练数据3000个,良性的数据有2700个,且其个体均是肿瘤大小比较小的,而另外300个恶性的,其肿瘤大小都很大,如果简单地认为 $P(A)$ 就是:$2700/3000 = 90\%$ ,那么现在每来一条新数据,是否可以不管其任何特征($x$,比如肿瘤大小)就认定其是A的概率就比B高呢?显然不能。
那么我们回到求 $P(A)$ 的问题上来。实际上,对于 $y$ ,只有 ${0,1}$ 两个值(二元分类,“非是即否”),我们要尽可能地让假想函数落在 $0\sim1$ 的区间里,而且最好是集中在 $0$ 和 $1$ 两头(因为$0.5$相当于两种可能性概率平分,无法预测),然后
$$
当h(x) \ge 0.5时,认为y(预测值)应该为1(是A),计算与实际值的偏差(cost) \\
当h(x) < 0.5时,认为y(预测值)应该为0(不是A),计算与实际值的偏差(cost)
$$
值得注意的是:这里的 $h(x)$ 计算的是 $P(A)$ ,即使 $h(x) < 0.5$ 也是表示——$y=1$的概率比较小,亦即:$y=0$的概率比较大。如:若某条新数据的$h(x)=0.2$,说明$y=1$的概率为$0.2$,也就是$P(A)=0.2$ ($y=1$ 和 $y$ 是
A是等价的表述),说明更可能是B。
这样就可以得出我们的代价函数-$Cost\ function$,继而通过梯度下降拟合出最优特征参数 $\theta$。
假想函数表达式-$Hypothesis\ Representation$
前面我们提到:对于 $y$ ,只有 ${0,1}$ 两个值,我们要尽可能地让假想函数落在 $0\sim1$ 的区间里,而且最好是集中在 $0$ 和 $1$ 两头。
通过逻辑函数 $Sigmoid \ Function$ 可以将假想函数的值限制在 $0-1$范围内。
$$
h_θ(x) = g(θ^Tx) \\
z=θ^Tx \\
g(z) = \frac 1 {1+e^{-z}}
$$
解释一下这个函数 $g(z) = \frac 1 {1+e^{-z}}$ :
$$
当z<0时,e^{-z}>1,0<\frac 1 {1+e^{-z}}<0.5\\当z>0时,0<e^{-z}<1,0.5<\frac 1 {1+e^{-z}}<1
$$
这个函数的图像如图:
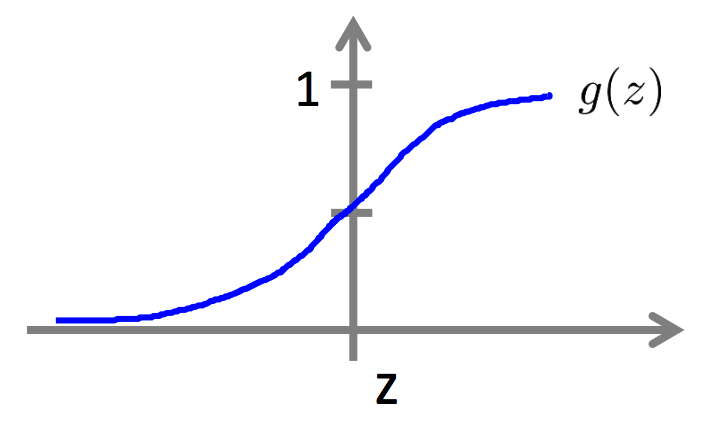
对于任意给定的 $ z = \theta^Tx $ 都能将 $h(x)$ 放缩到 $0 \sim1 $ 之间,且集中两头,非常符合我们的要求。
这个函数有时候也会写成:$g(z) = \frac {e^z} {1+e^z}$,是一样的,只是简单转化了一下,消除了了 $z$ 的负号
$$
g(z) = \frac 1 {1+e^{-z}} = \frac 1 {1+ \frac 1 {e^z}} = \frac 1 { \frac {1+e^z} {e^z}} = \frac {e^z} {1+e^z}
$$
决策边界-$Decision\ Boundary$
考察假想函数的 $z$ 的取值范围,可以对 $z=\theta^Tx$ 做特征值 $x$ 的取值分析:
以两个特征为例:
情形一:
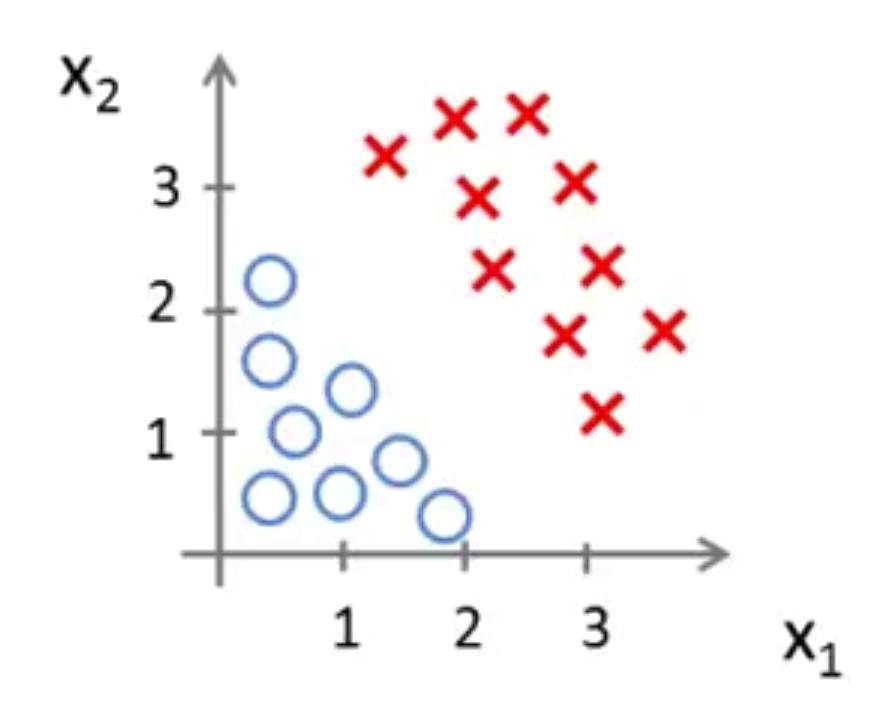
令 $x_1、x_2$ 满足 $z=\theta_0+\theta_1x_1+\theta_2x_2$ 这样的线性关系,通过梯度下降拟合,最终得到一条下面的直线就很理想了,以直线为决策边界,直线一边 $z>0$ 是 $y=1$,另一边就是 $y=0$
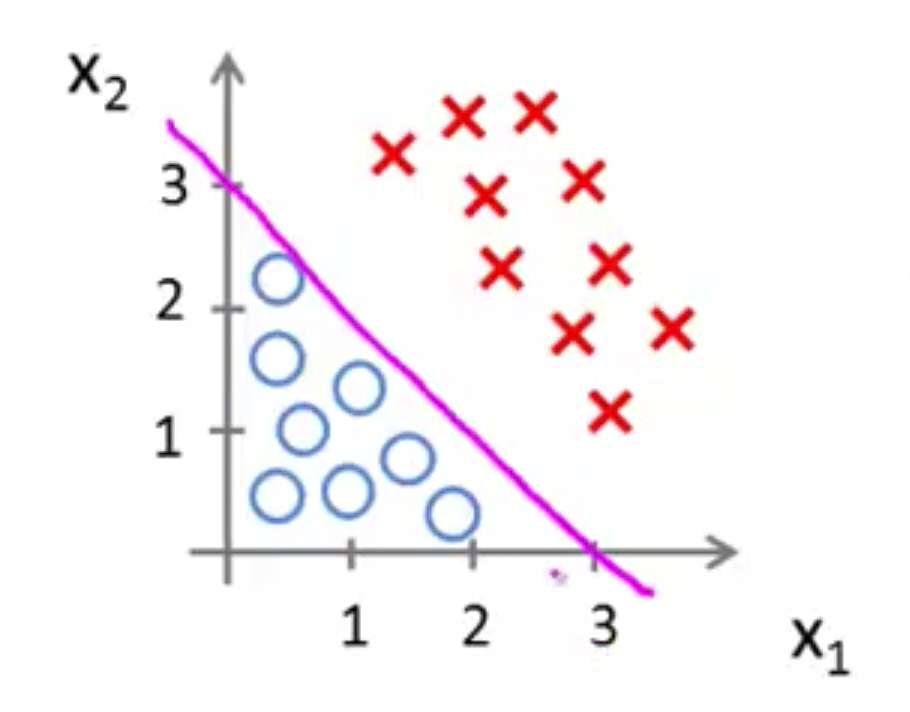
情形二:
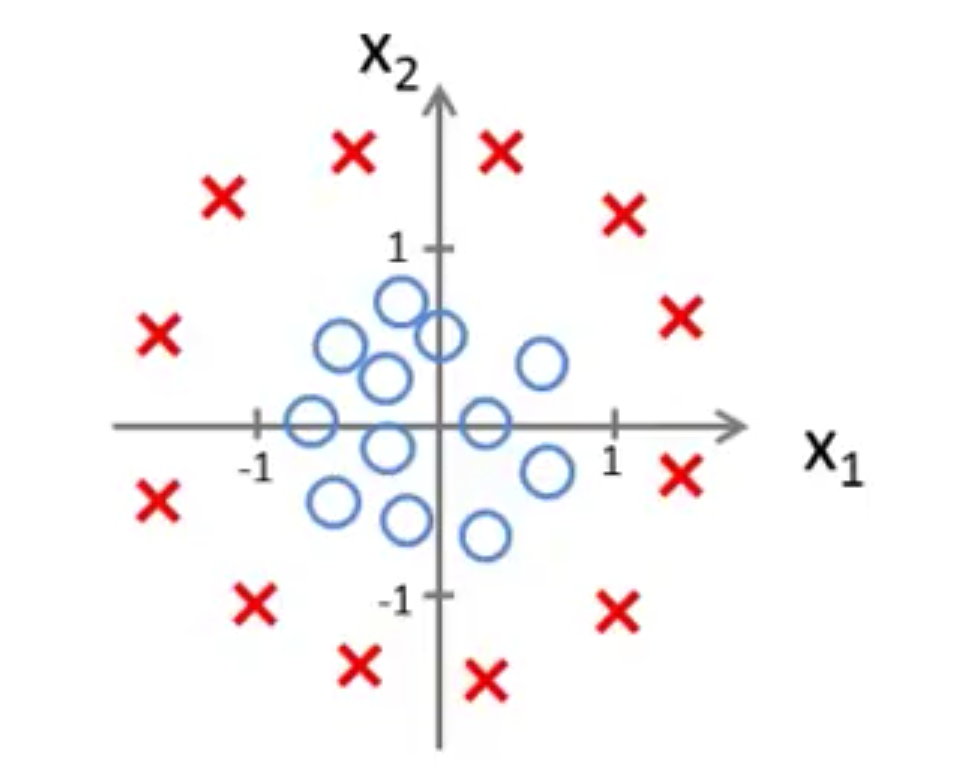
这样的数据,$x_1、x_2$ 就无法构成线性关系,使用高次多项式 $z = \theta_0+\theta_1x_1+\theta_2x_2 + \theta_3x_1^2+\theta_4x_2^2$ 来拟合出一个圆,以圆作为决策边界,圆内 $z\lt0$ 为 $y=0$,圆外 $z\gt0$ 为 $y=1$
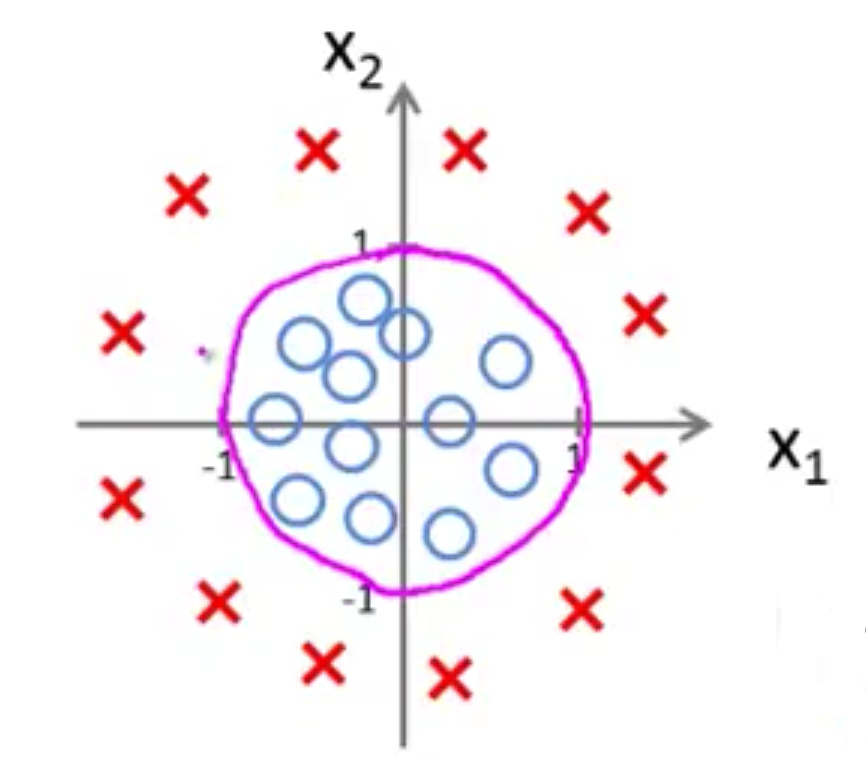
考察决策边界有两方面的作用:
- 让我们更好地选择合适的假想函数,正如我们在处理线性回归的时候:如果数据点集看起来像一条直线,我们就是用线性函数,而如果点集看起来更弯曲,我们就需要考虑使用多项式函数。
- 起到一定的预测作用,决策边界已经能大致给出不同分类结果所对应的 $x$ 的位置或范围,对于新数据,用按图索骥的方法基本能得到结果了。
但其实,决策边界是在得出特征参数 $\theta$ 之后才能真正算出来的,但是对决策边界的前期考察是可以产生上述的良好效果的。
代价函数-$Cost\ Function$
之前提到: $h(x)$ 经过了放缩,所以计算 $cost$ 的时候,$cost$ 也会被缩小——两个 $0\sim1$ 之间的数,作差再平方,基本就没了。
这就导致 $J(\theta)$ 很容易达到一个局部最小值,为了避免这种情况,需要再次放缩,将 $cost$ 放大:
指数和对数永远都是一对好基友,用指数缩小的,那就用对数来放大吧!
$$
\begin{matrix}
当y=1时,h(x)越接近1,cost 应该越小,反之越偏离y,产生的cost就应该越大\\
当y=0时,h(x)越接近1,cost 应该越大,反之越偏离y,产生的cost就应该越小
\end{matrix}
$$
所以需要分类讨论:
$y=1$ 时,$Cost(h)$ 应该是个递减的函数;
$$
Cost(h) = -log(h(x))……log:以10为底的对数
$$
图形直观: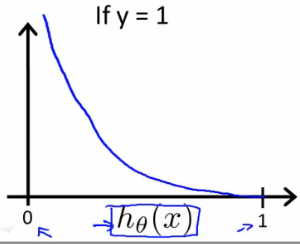
偏离 $1$ 越远,代价越大。
$y=0$ 时,$Cost(h)$ 应该是个递增的函数;
$$
Cost(h) = -log(1-h(x))
$$
图形直观: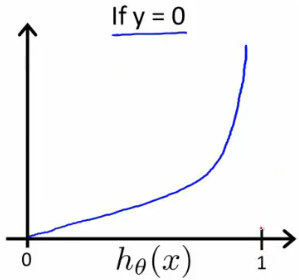
偏离 $0$ 越远,代价越大。
对每一个代价求和就可以得到代价函数 $J(\theta)$ ,但是分段函数求和、求导都很麻烦,我们用一种特殊的技巧,将上述两种讨论合而为一, 这样,就得到了我们的总代价函数:
$$
J(\theta) =\frac 1 m \sum_{i=1}^mCost(\theta,x)= \frac 1 m \sum_{i=1}^m(y·log(h(x)) +(1-y)·log(1-h(x)))
$$
读者可以将 $y=0$ 和 $y=1$ 分别代入,验证是否符合上述两种分类中的讨论。
梯度下降-$Gradient\ Descent$
按照传统的步骤,要对代价函数进行求导。
下面是对 $J(\theta_j)$ 的求导过程:
$$
\begin{align}
\frac \partial {\partial\theta}J(\theta_j)
&=-(y·\frac 1 {h(x)} -(1-y)·\frac 1 {1-h(x)})·\frac \partial {\partial\theta}h(x) \\
&=-(y·\frac 1 {h(x)} -(1-y)·\frac 1 {1-h(x)})·(-(1+e^{-z})^{-2})·\frac \partial {\partial\theta}e^{-z} \\
&=-(y·\frac 1 {h(x)} -(1-y)·\frac 1 {1-h(x)})·(1+e^{-z})^{-2}·e^{-z}·\frac \partial {\partial\theta}(\theta^Tx) \\
&=-(y·\frac 1 {h(x)} -(1-y)·\frac 1 {1-h(x)})·(1+e^{-z})^{-2}·e^{-z}·x_j \\
&=-(y·\frac 1 {h(x)} -(1-y)·\frac 1 {1-h(x)})·(1-h(x))·{h(x)}·x_j \\
&=-(y·(1-h(x))-(1-y)·h(x))·x_j \\
&=(h(x)-y)·x_j \\
\end{align}
$$
注:理论上,$log(x)$ 求导不应该是 $\frac 1 x$ , $ln(x)$ 才是,但其实以 $10$ 为底,还是以 $e$ 为底,对结果并没什么影响,所以我们就不管它。
这中间要用到前面的一些公式,点击传送:$Sigmoid$、$J(\theta)$。
原来即使 $J(\theta)$ 变得花枝招展,梯度下降的公式还是一样的啊!