数位迭代、牛顿迭代、二分法?有多少种方法可以求一个数的平方根?
背景介绍
数学和计算机科学总是能够在“拐角遇到爱”,计算机以其强大到离谱的高计算能力帮助人类在数学创新上不断突破,而数学上的成就也总能在理论上提供计算机发展的不竭动力。
数学上对于五次方程没有根式解的结论已经得到证明。高次方程的求解一直是数学上的难题,而这个问题在航天、工程、医学等领域都有着极其重要的应用,当然这必然要用到计算机强大的运算能力。
人们在计算四则运算的时候就能体会到,随着计算法则的升级,人力所能做到的运算,越来越有限,于是在开平方这个问题上,人们一直没有找到特别好的办法,来处理不能完全开方的数—因为开出的数为无理数。但有一点值得庆幸的是,人们可以想到各种方法来逼近无理数方根的值。
逼近方根解
数位递减迭代
- 最初我在考虑这个问题时,并没有采取更加合理的“二分法”—当然,我本人也说不出为什么,可能是希望想到更优的算法,也可能只是喜欢异想天开……
- 首先我想到的是,0-9的平方结果不会超过100,然后我观察到一个规律:0-9的平方是两位数,10-99的平方是4位数,100-999的平方是6位数……
- 这也就意味着,整数位的位数会直接决定方根整数位的位数,这之间也许存在着可以运算求解的空间。于是我开始了演算。
- 大致描述一下迭代的过程:
- 给定一个数12345,求方根;
- 这是一个5位数,方根应该是一个3位数,所以假设最高位为x(取值0-9),后两位构成y(取值0-99);
(100x + y)² = 12345 --> 10000x² + 200xy + y² = 12345 1⃣️ - 一眼就可以看出来,x = 1;
- 然后就可以得到:
10000 + 200y + y² = 12345 --> 200y + y² = 2345 - 这个时候式子反而复杂了—😳
- 不要这么快就放弃,继续探索,求第二位。
- 这里意识到:现在变成了求y的首位数字了;
- 那么继续假设y的首位数字是x₁(0-9),最后一位则为y₁;
- 于是有:
200 * (10x₁ + y₁) + (10x₁ + y₁)² = 2345 2⃣️ - 这个式子展开似乎不是很理智,当然可以摸索阶段可以试试,得到:
100x₁² + (2000 + 20y₁)x + 200y₁ + y₁² = 2345 - 不过到这里,我有了更好的方案,位数关联可以做到更细一点,考虑到乘法是有进位的,也就是说,在1⃣️式中x²是不会大于12345对应的5-6位上的数–‘1’的;
- 亦即:
x² ≤ 1 3⃣️ - 所以x只能为1(首位不为0);
- 对于2⃣️式,是否也有这样的考虑?
- 这个时候如果继续去执着于y₁这个个位数显然是舍本逐末了,我们可以将12345缩小100倍,变成123.45,不考虑多余的0.45的话,2⃣️式会简化很多:
(10 + x₁)² = 123 --> 100 + 20x₁ + x₁² = 123 --> 20x₁ + x₁² = 23 4⃣️ - 当然,这里其实应该用≤更合适,取其极限值就可以了;
- 这样的式子,x₁在0-9范围内是很好遍历去计算结果的,得到x₁ = 1;
- 要想继续迭代,首先要回过头来看3⃣️和4⃣️两个式子,找到它们统一的表达方式;
- 4⃣️式中多一个20x₁,这个20怎么来的呢?回头搜索一下可以发现,是前一位x在加和平方时得到的,那3⃣️式为什么没有这一项?我们想到首位x前面没有数了,也就是说,是0,所以3⃣️式严格来说要写成:
0 * x + x² ≤ 1 - 那么迭代式是不是就是:20x𝓃 * x𝓃+₁ + x𝓃+₁² = num ?
- 很遗憾,并不是,仔细去摸索会发现,蓝色那个数值是会在迭代过程中累计的,并不是只依赖上一位数值,原因呢我大致写几个式子看一下:
- 第一位:(0 + x)² ≤ 1 —> x = 1;
- 第二位:(10 + x₁)² ≤ 123 —> x₁ = 1;
- 第三位:(110 + x₂)² ≤ 12345 —> x₂ = …
- 这样一看就很清晰了吧!
- 但是要注意:这种清晰的逻辑在计算机处理过程中很容易溢出!所以我并没有直接这么做。
代码实现:
二分法—原来可以这么简单!
- 二分法,是逼近求根问题中经常用到的一种数学方法。
- 很多人听说过“二分法”,像我们所熟知的“猜数字”。猜数字的时候,有一个技巧,可以帮助我们相对快速地得到准确答案。
- 比如现在猜一个0-100的数:
第一步,猜50;
大了,就说明这个数在0-50之间;
第二步,猜25;
小了,就说明这个数在25-50之间;
依次类推,一直猜中间的数,可以有“目的性”地快速找到正确结果 - 二分法就是这个原理。
- 但是这里会有一些问题:
大于1的数,方根比原数小
小于1的数(>0),方根比原数大 - 所以代码上需要加以判断区分。
代码实现:
进阶—牛顿迭代法
- 我先举个简单的例子来描述一下这样的场景:
- 在你面前,有一个球体,比如说这样的:

- 相信大家对于这种类似的球体,尤其是大型的,会有一种感觉,就是球底部接近地面的地方,总是会照不到阳光。
- 如果有观察的比较细致的同学,可能会发现更奇妙的事情,随着阳光的推移,照射到球体产生的阴影会变大、变小,就是大概这样一个过程:
- 仔细一看,这道光线其实是在逼近底部那个我们想照到的位置的。
- 贴着球面的那道光线,我们称之为“切线”。其实很多曲线的切线都有这样很直观的感觉,要求二次方根,去探索二次函数的曲线是个比较靠谱的思考方向。
- 那么,我们就来看一下下面这幅图:
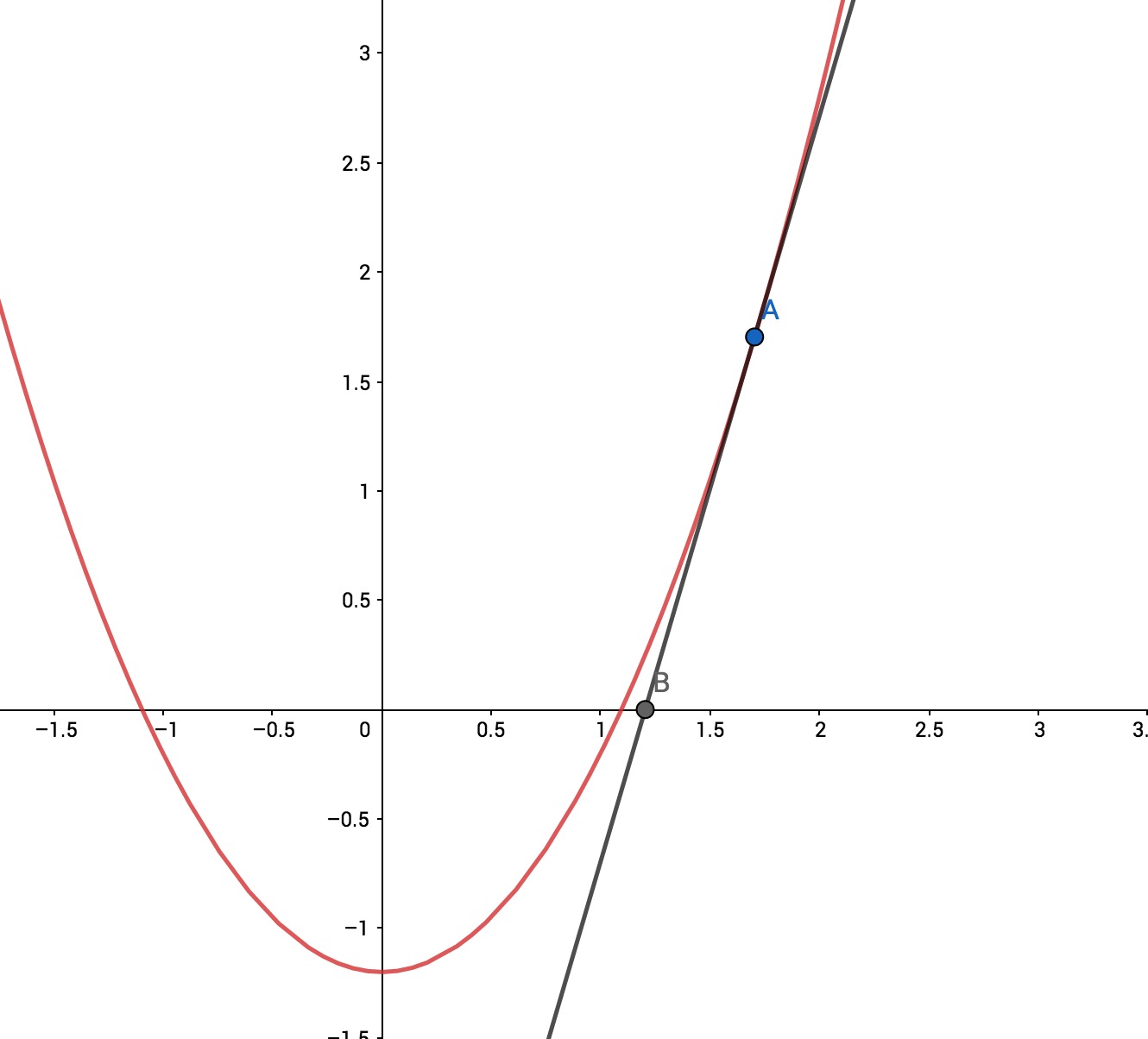
- 二次方根是可以逼近的。
- 只要能根据A处的切线,求出B点的坐标,我们就可以顺着这个思路走下去了。
- 思路有了,然后就需要有一些知识储备来完成我们的想法了。首先,就是切线,这个东西呢,和导数有关,导数呢,又和微积分有关,牵扯太多,我们暂不管这些~我们只需要以太阳光照射一个弧面产生阴影的例子来理解就好了。
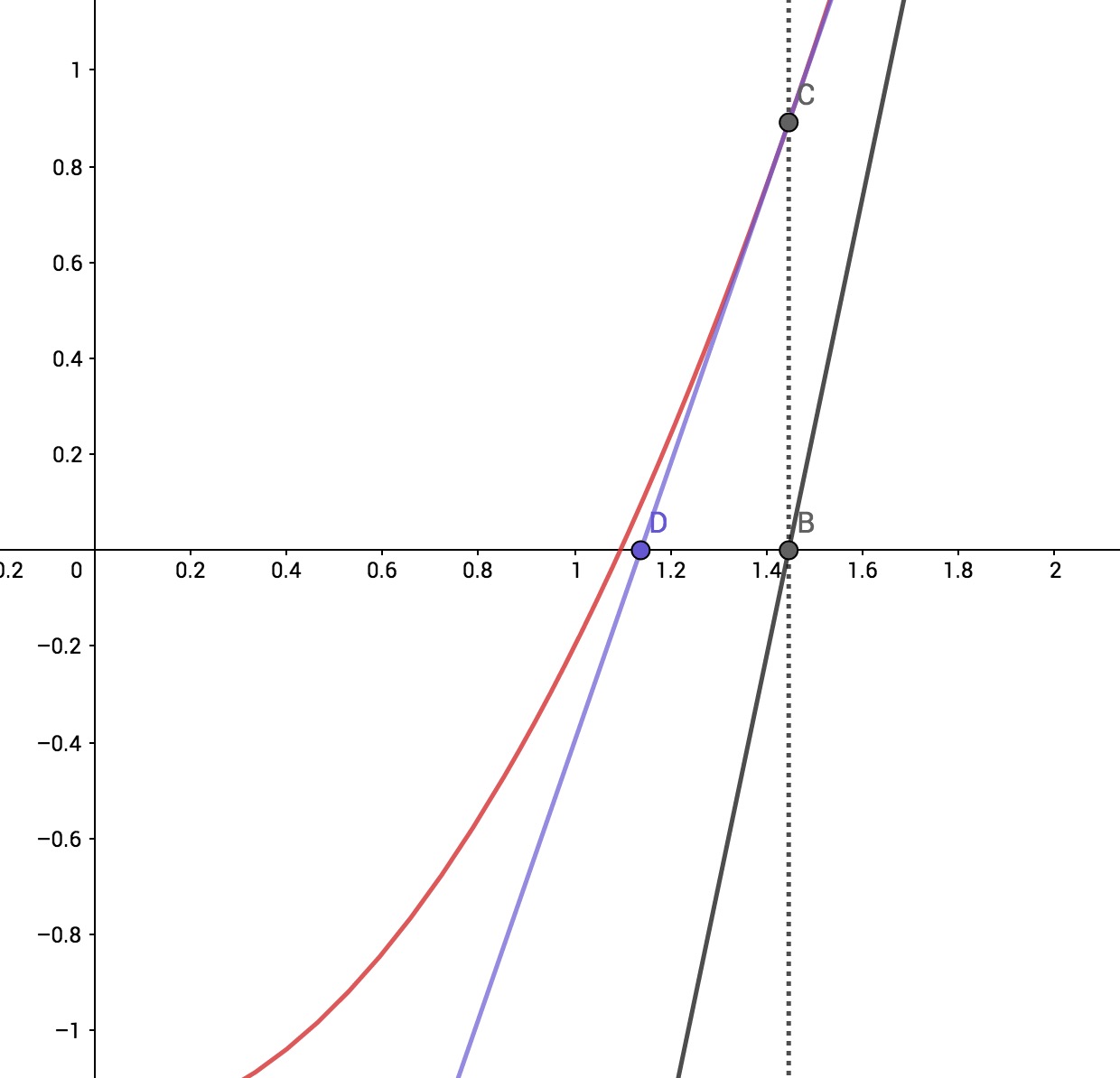
- 现在假设我们有了求切线的工具,可以得到下图B点的位置了,这样,B点显然要比A点离根值点近了,然后我们再以B点为准,找到二次函数曲线上对应的C点,再做一次刚才的步骤,得到D点,D点又更加接近了。
代码实现:
网上有现成的公式,不过,有兴趣的同学可以自己推导一遍。
→牛顿迭代求平方根←
本文可以参考: